to top
Technical Notes on Statistics and Estimation Theory
-
Gauss--Helmert Model as Optimization Problem
[bibtex]
[pdf]
-
Pre-calibration and in-situ Self-calibration with Correlated Observations
[bibtex]
[pdf]
[cdy]
-
The Mean of Correlated Observations
[bibtex]
[pdf]
-
Accuracy of the Mean when using a Wrong Covariance Matrix
[bibtex]
[pdf]
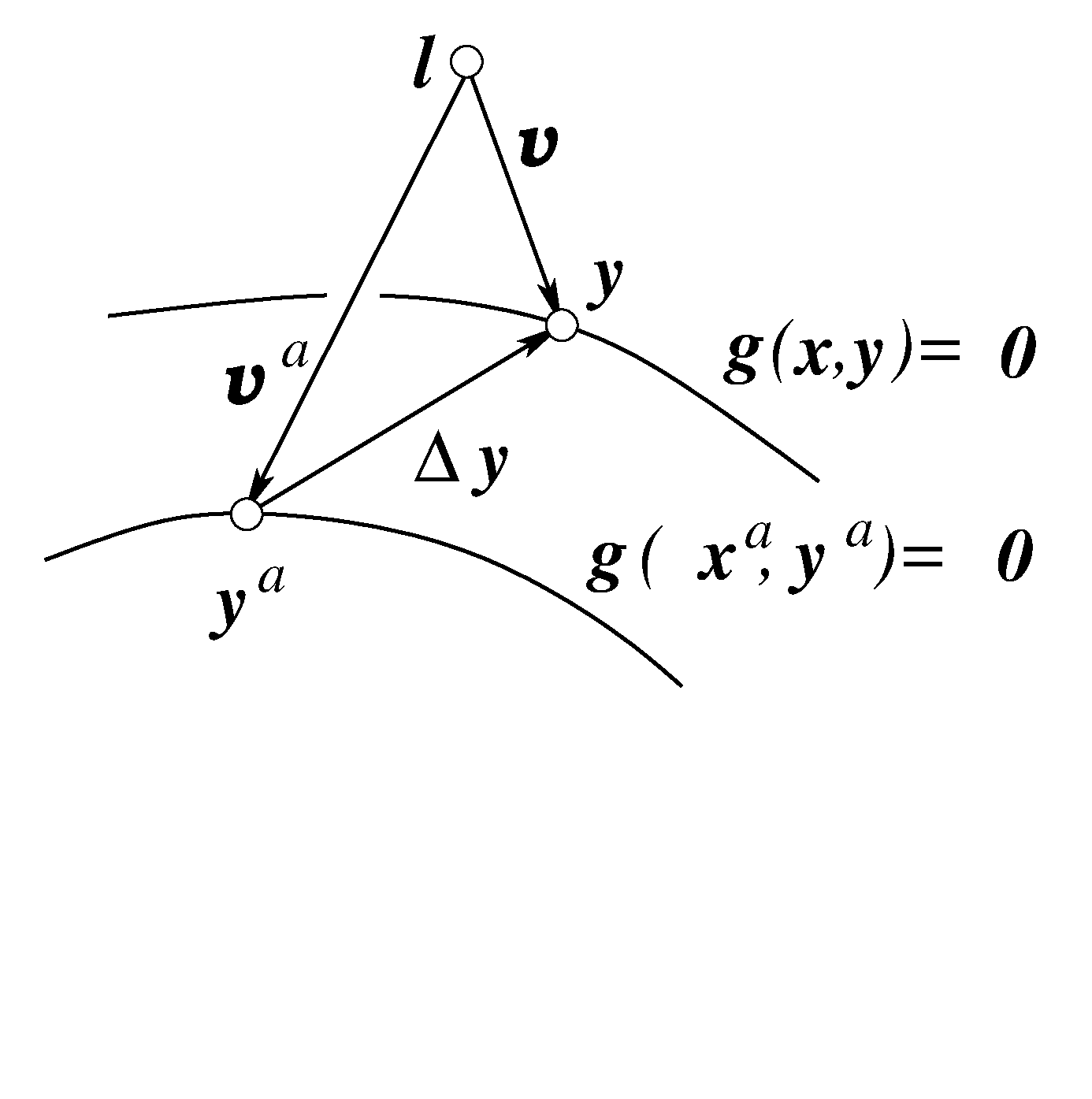 |
The Gauss--Helmert generalizes the well-known Gauss--Markov model by allowing implicit relations between the observations and the unknown parameters. The classical derivation of the estimation procedure refers to the statistical nature of the Maximum-Likelihood optimization. The note separates the description of the model and the optimization function from the generally iterative numerical optimization procedure, in order to elucidate the non-statistical properties of the intermediate steps before treating point of convergence as final estimate. |
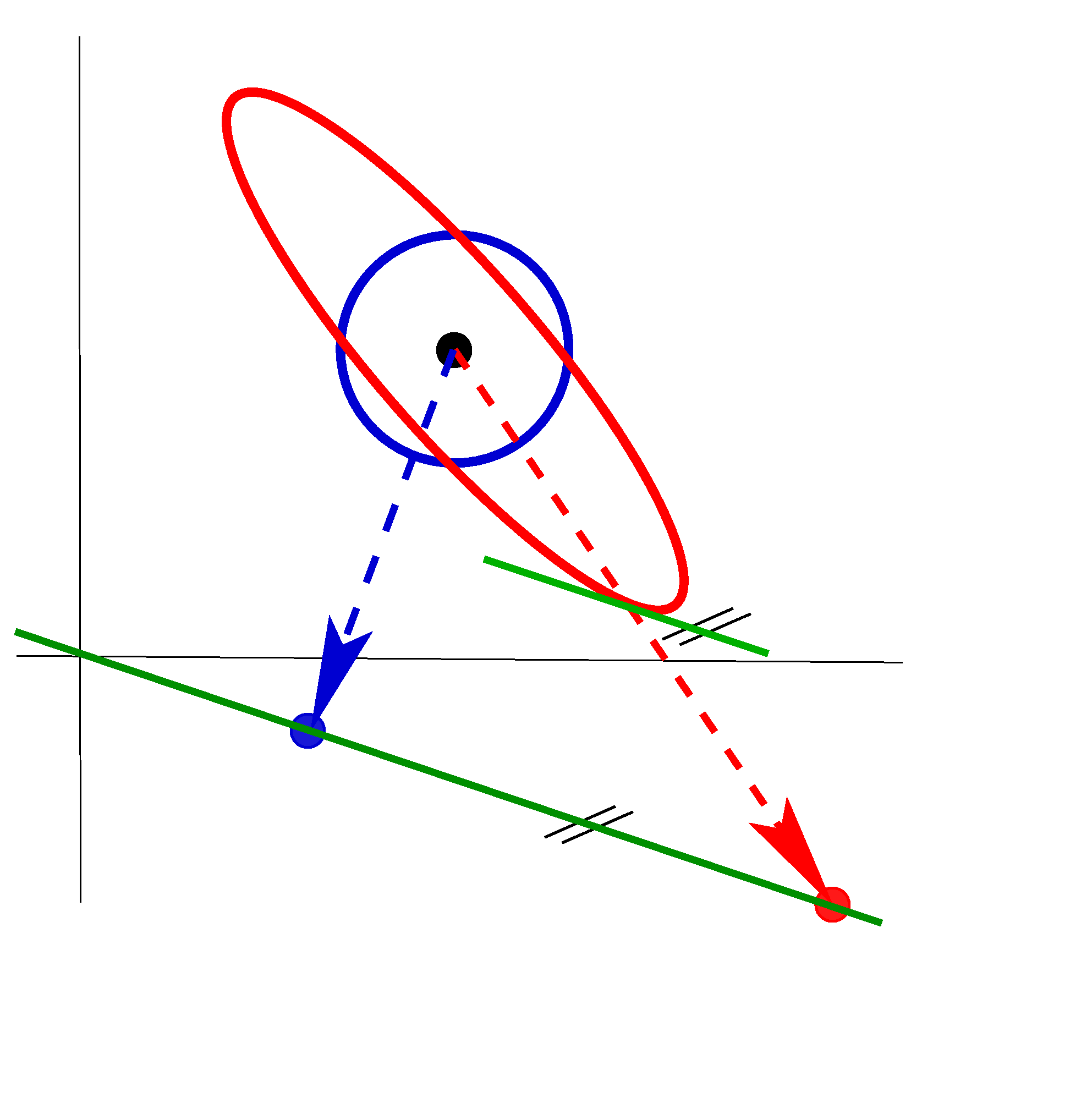 |
Deformation analysis based on point clouds taken at different times may require to take into account both preclalibration and in situ self-calibration of the used instruments. We analyse the mutual effect of pre-calibration and in-situ self-calibration w.r.t. (1) the necessity to exploit the full covariance structure of the point cloud induced by the pre-calibration and (2) the possibility of increasing the computational efficiency during the self-calibration. |
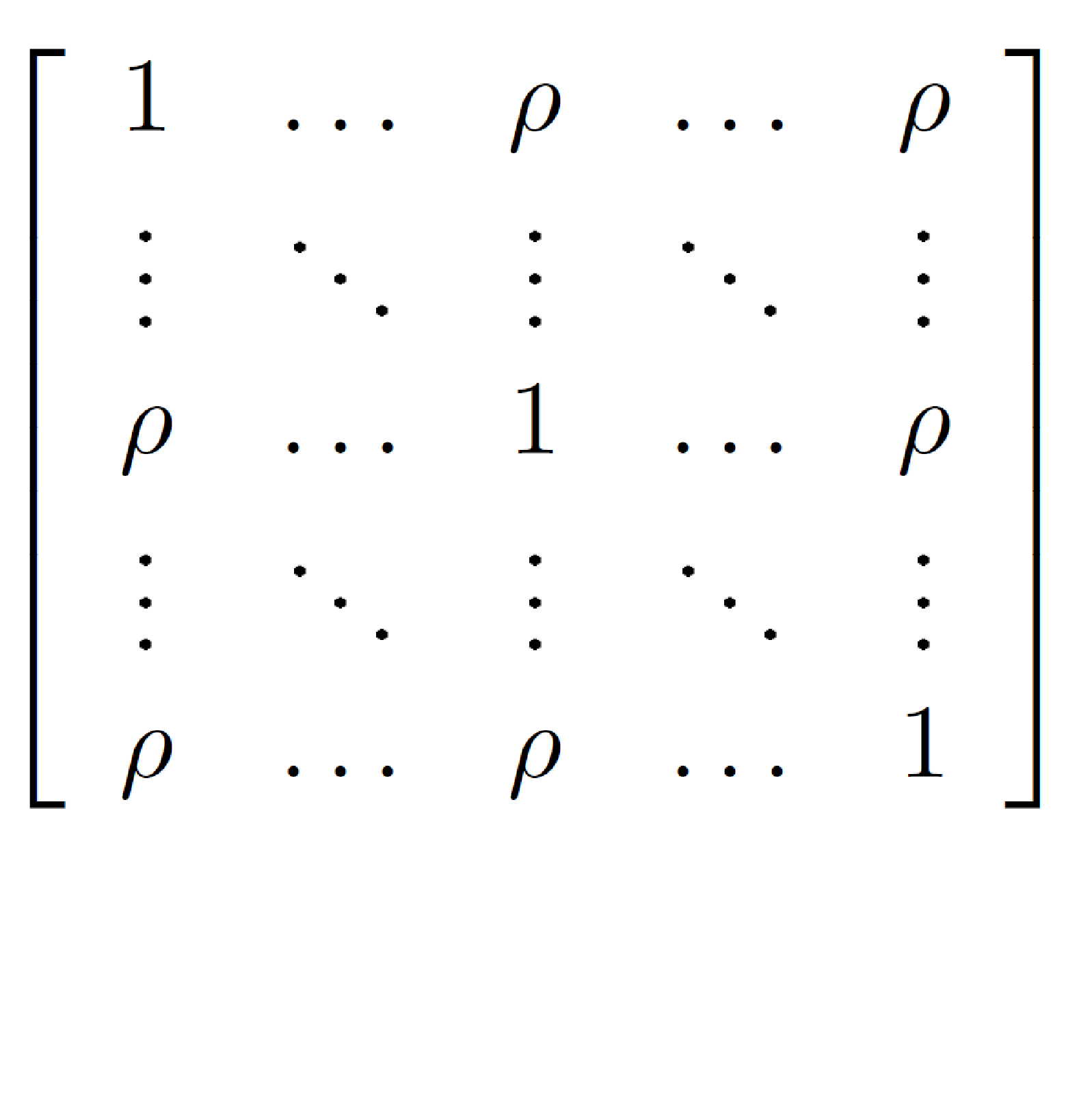 |
For uncorrelated observations the accuracy of the mean increases with the number of observations. In case they are correlated, there is an upper limit for the accuracy. The note analyses the situation for constant correlation and for exponentially decaying correlation, autoregressive noise. |
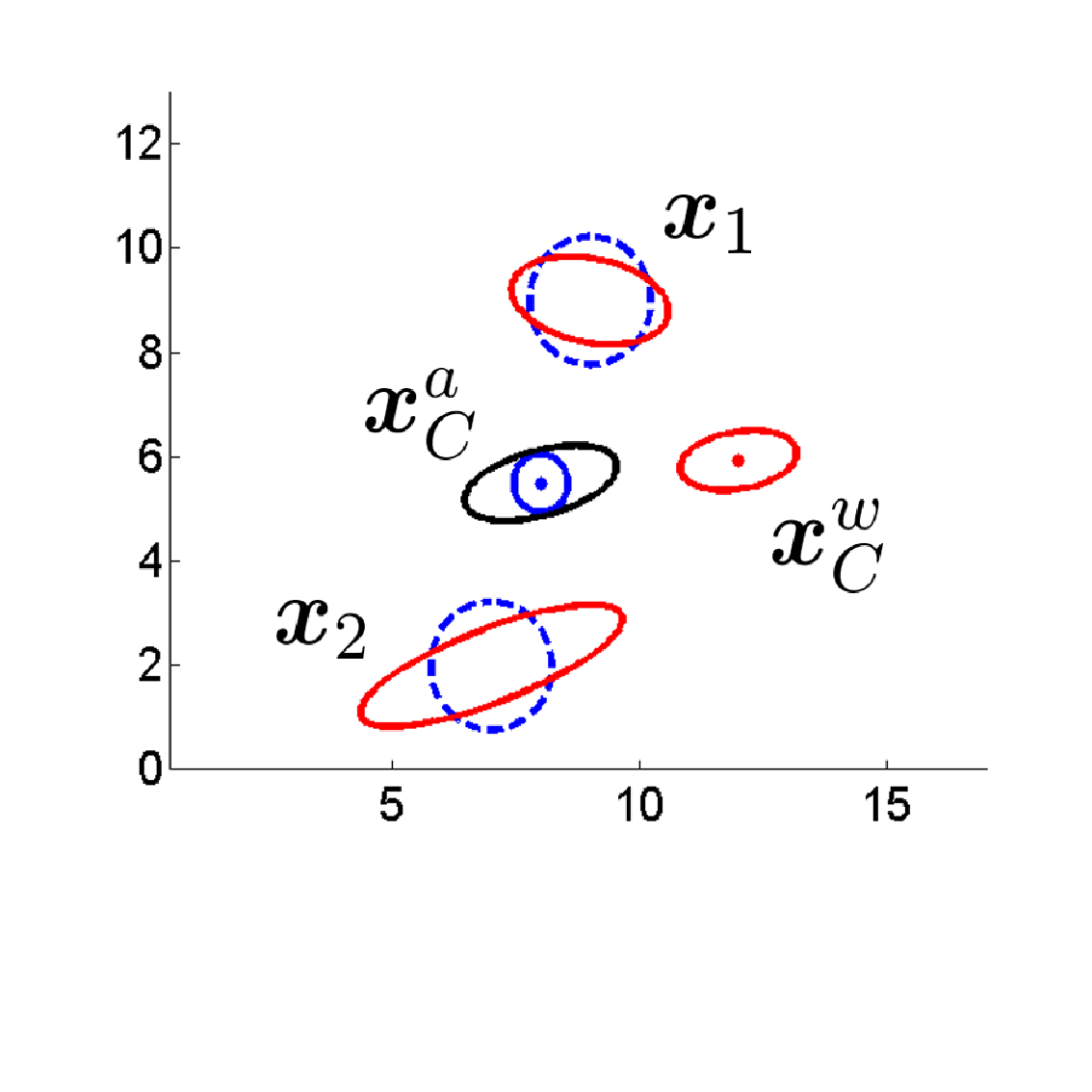 |
Suboptimal, i.e., approximate solutions often are used or needed when estimating parameters. One of such simplifications refers to the stochastical model, especially the covariance matrix of the observations, which often is assume to be a multiple of a unit matrix, implicitly assuming all observations have the same weight and are mutually uncorrelated. This note provides the general relation between the accuracy of the estimated parameters when using an approximate covariance matrix and exemplifies this using the mean of repeated observations. |
to top
Technical Notes on Estimation of Geometric Entities
-
Motions and their Uncertainty
[bibtex]
[pdf]
[code]
-
Centroid Form of an Uncertain Plane
[bibtex]
[pdf]
-
Planes from Points
[bibtex]
[pdf]
-
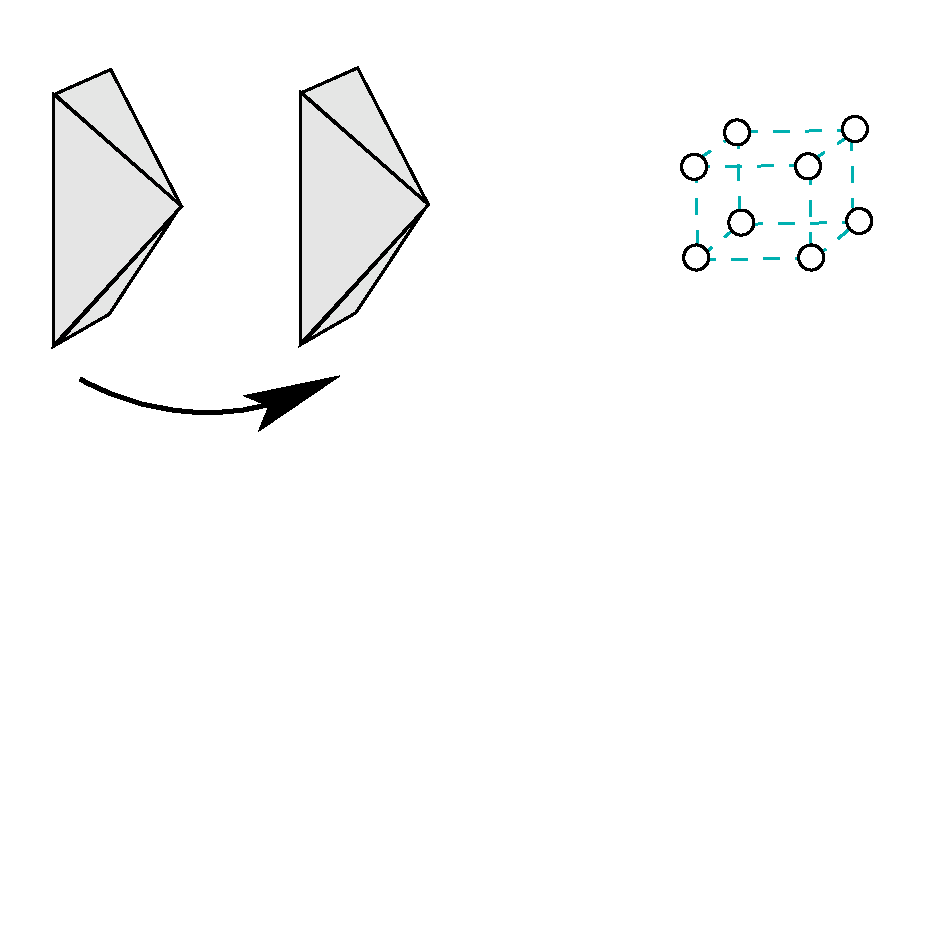
Direct Solutions for the Similarity from Plane Pairs
[bibtex]
[pdf]
 |
We addresses the ambiguity of representing uncertain motions. We analyse the relation between an exponential representation with a homogeneous 4x4 matrix and the representation with a rotation matrix, also represented exponentially, and a translation vector. The rotation parts turns out to be identical, while the translation parts differ, why a transparent documentation of the motion representation is necessary. As a sideline, the note addresses the inversion, the concatenation, and the difference of uncertain rotations and uncertain motions. |
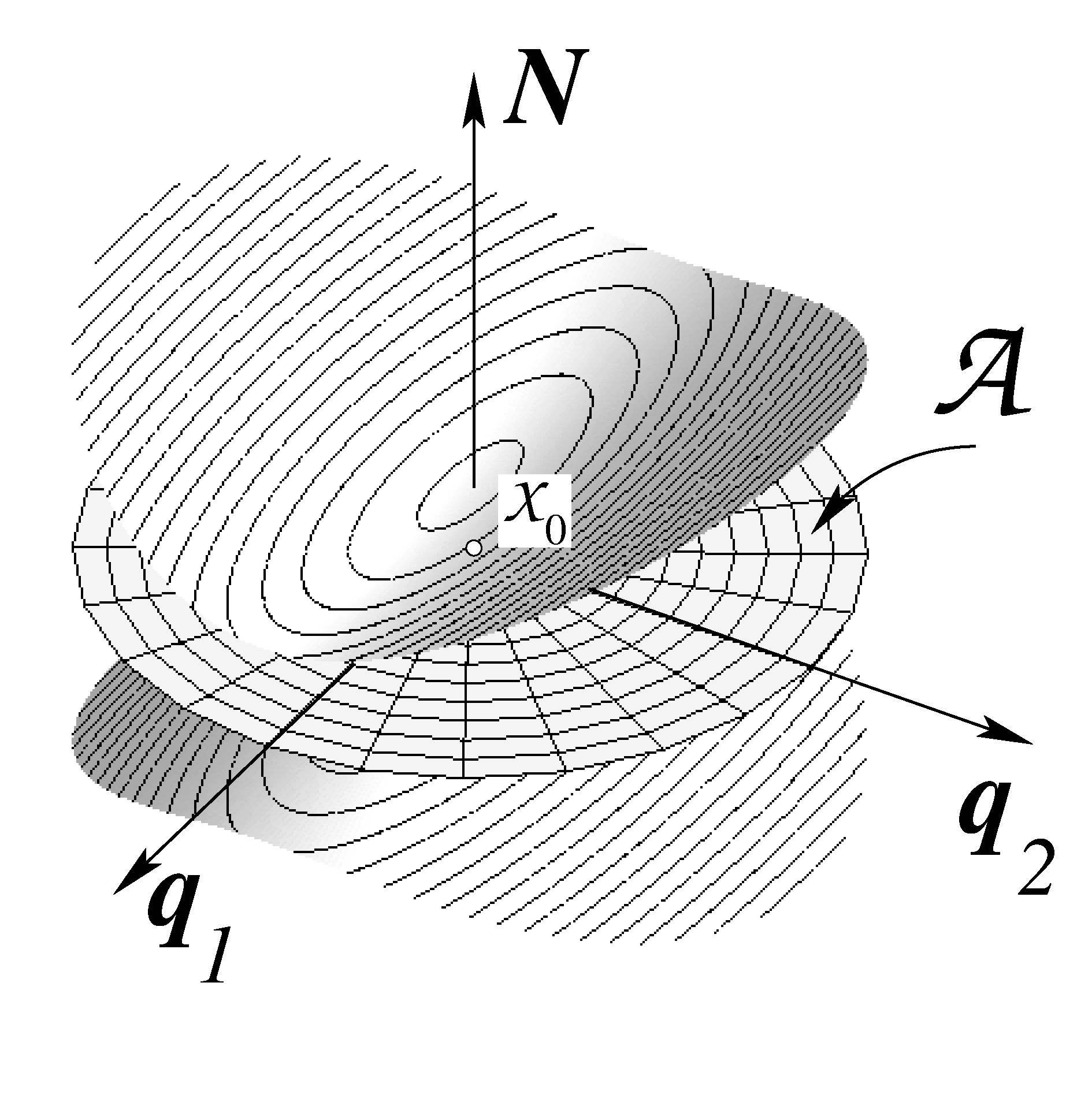 |
A plane can be represented in various manners. We especially discuss the centroid form of an uncertain plane, which naturally results from estimating a plane from a given point set. We discuss the representation, its recursive estimation assuming isotropic point uncertainty and optimal estimation. |
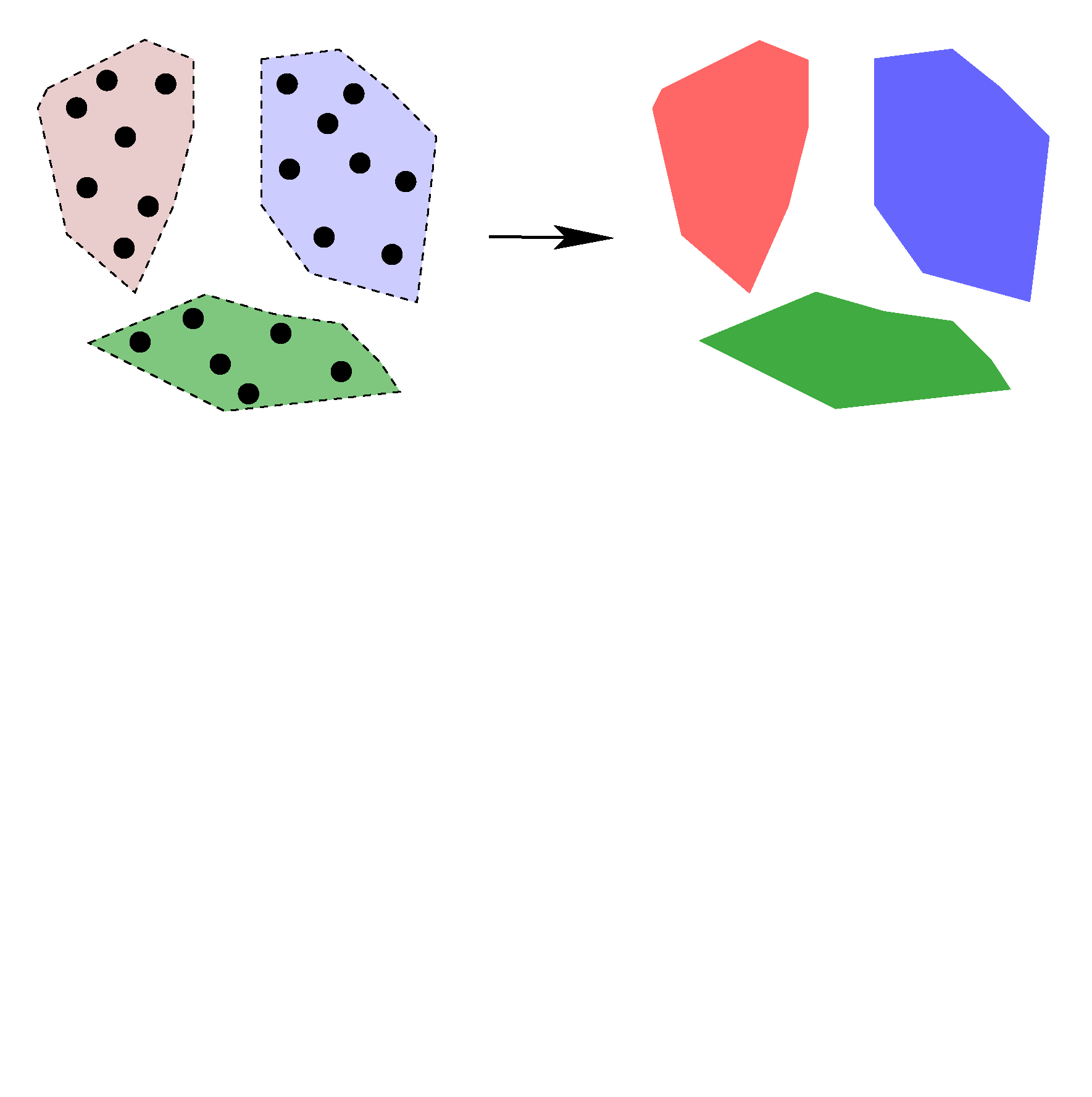 |
We describe the statistically optimal estimation of a single and of multiple planes from a point cloud, where the full covariance matrix of all scene coordinates is available, e.g., from bundle adjustment. This procedure might be used to derive ground truth data for plane extraction or for homography estimation. |
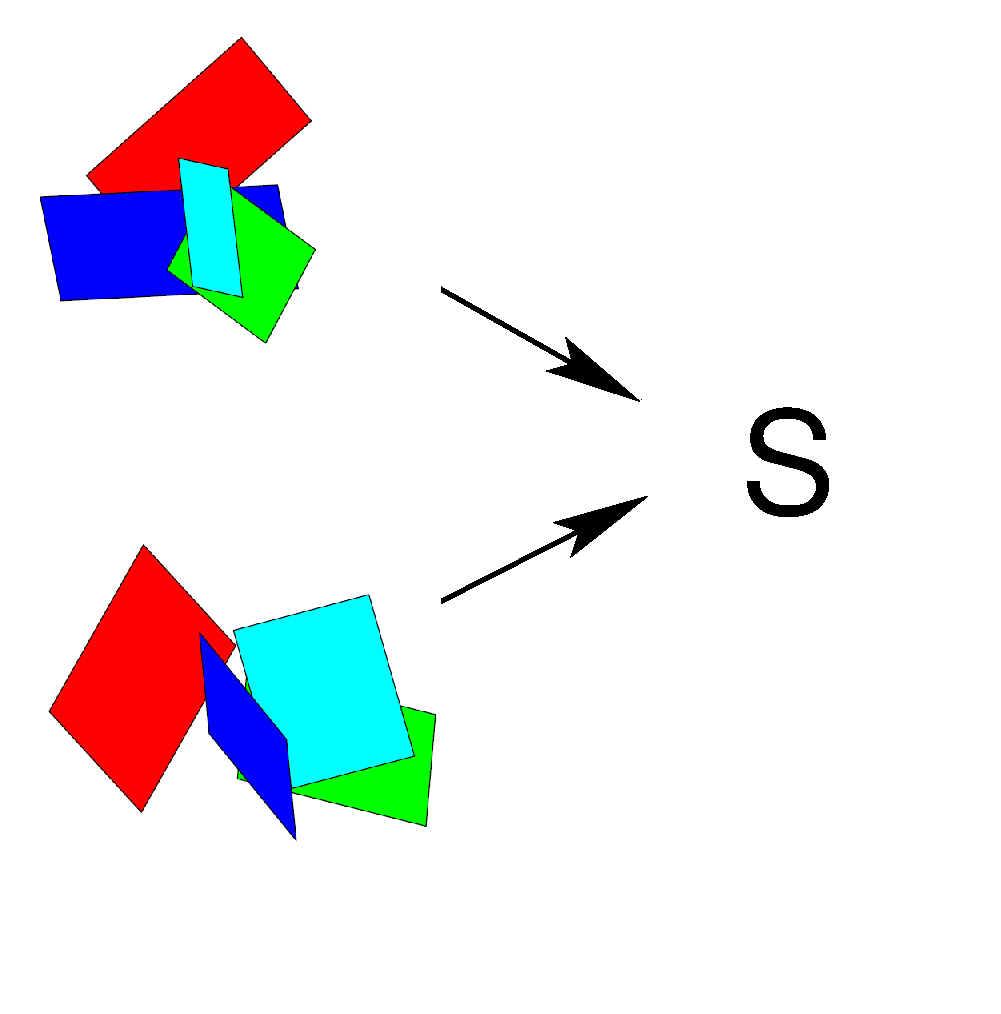 |
We collect some direct solutions for determining the similarity (or motion) from corresponding plane pairs, representing point clouds. Some of the solutions are able to handle the case, where the sign of the normals are not consistent. |
to top
Technical Notes on Bundle Adjustment and Surface Reconstruction
-
Rule of Thumb for Precision of Points from Multiview Triangulation
[bibtex]
[pdf]
-
Multi-View Triangulation with Directions
[bibtex]
[pdf]
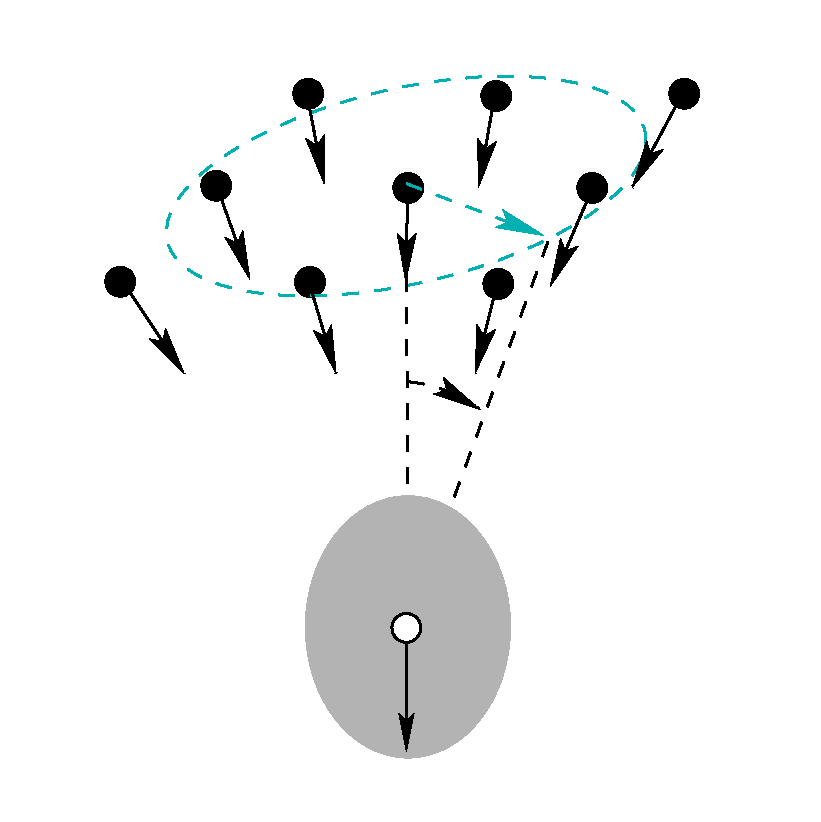 |
For planning bundle adjustment configurations, the expected accuracy of triangulated points is an essential ingredient. We derive rules of thumb for the accuracy of multi-view triangulating by providing simple expressions for the depth and lateral accuracy of 3D points, for images arranged in a line, in a planar region and in a spherical region, covering the case of omnidirectional cameras. |
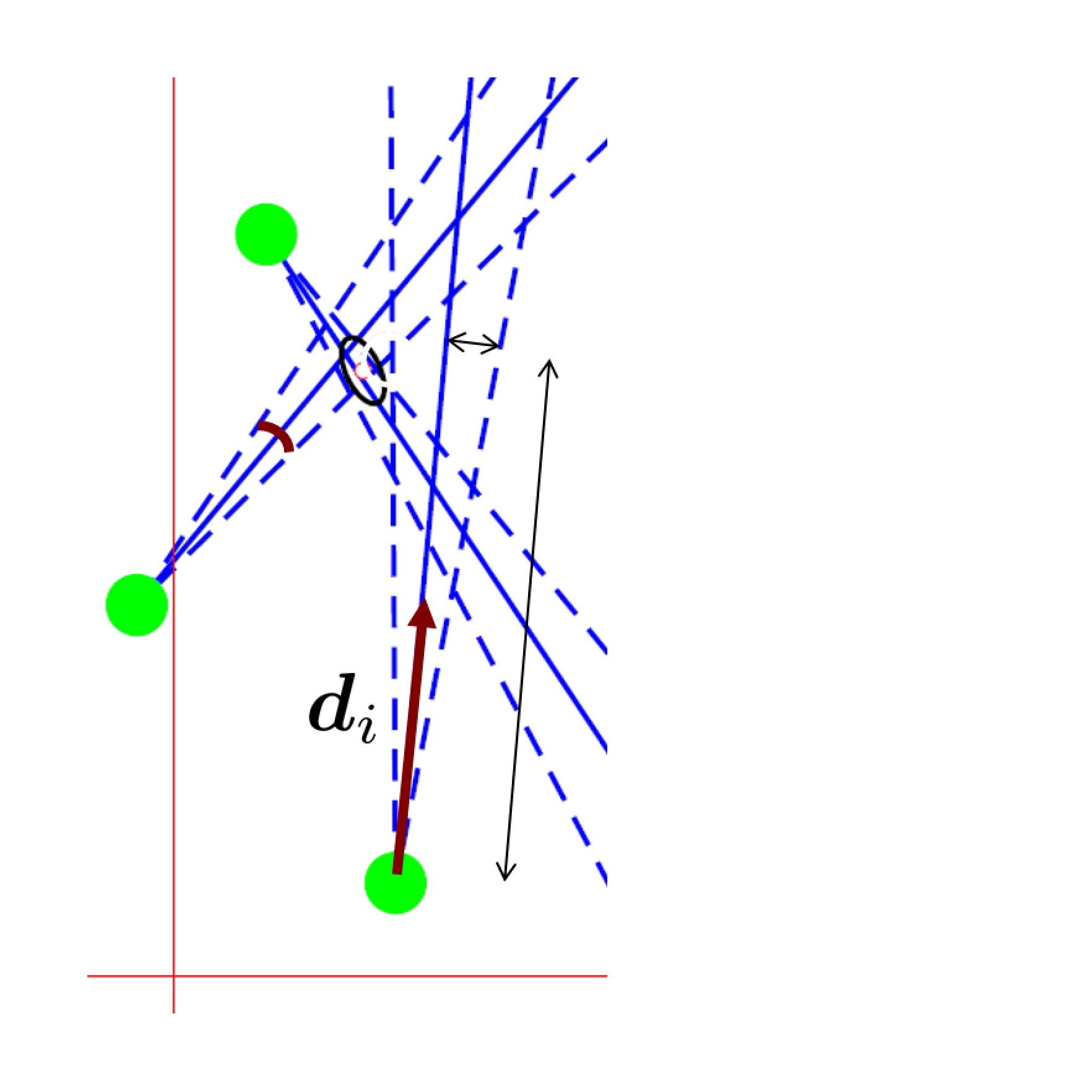 |
We provide simple solution to the optimal triangulation of a scene point from multiple views assuming isotropic uncertainty of the directions. As a special case we provide a simple expression for the distance of the triangulated point in case of homogeneous directional uncertainty and small basis, expressed as a function of the effective base line, the viewing angle and the resolution of an omnidirectional camera and the matching accuracy in pixels. |